最近こちらの書籍を読んでいます。

コンピュータシステムの理論と実装 ―モダンなコンピュータの作り方

Amazon

こちらの本は一言で言うと「NANDからTetrisへ」

基本的な構成要素である論理ゲートからALU,CPUと作っていき、最終的にはアプリケーションであるテトリスを０から作ってみることでコンピュータの働きを理解すると言ったテーマになっています。

私もこの本に触発されてNANDゲートを基本にして、その他の論理ゲートを作成することを試みました。今回のブログはNANDの作り方、及びNANDから基本ゲートをどのように作成したかを記録したものになります。

前提となる用語
実装の流れ

前提となる用語

真理値表

複数の入力に対し、出力の結果を0,1で表現した表のこと。

下記はNANDの動作を表現した例

a	b	out
0	0	1
0	1	1
1	0	1
1	1	0

ブール関数

ある入力に対して、0か1を返す関数のこと。

論理ゲート

ブール関数を実装するための物理デバイスのこと。

例えばNANDの論理ゲートは下記の通り。

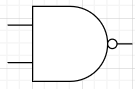
本ブログでは物理的には作らないが、

シミュレーションとして論理ゲートに相当する関数を作成し組み合わせて他の論理ゲートを作成していく。

基本論理ゲート

論理ゲートのうち、AND,OR,NOTの論理ゲートのこと

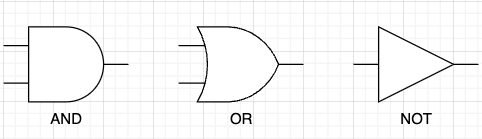
本ブログではNANDから上記三つを作成します。

実装の流れ

NANDゲートを作る

なんでNANDゲートを基準にするのか？

NANDゲート*1には面白い性質がありまして、NANDゲートさえあれば他の論理ゲートは全て表現できると言う性質があります。

今回はその性質を利用して、まずはNANDゲートを普通に作成し、その他の論理ゲートはNAND、もしくはNANDから作成した別のゲートを組み合わせて他のゲートが作れるかを試していきます。

NANDゲートの作成

では早速NANDゲートを作成しましょう。 NANDゲートは次のような動きを行う論理ゲートになります。

a	b	out
0	0	1
0	1	1
1	0	1
1	1	0

これをpythonで表現すると次のようになります。

def Nand(a:bool, b:bool) -> bool:
    return not (a and b)

テストもしていきましょうか。

from tools import gate
import pytest
import itertools

in2 = list(itertools.product([0,1],repeat=2))

expects = [1,1,1,0]
@pytest.mark.parametrize("a,b,expect",
   [x + (y,) for x, y in zip(in2, expects)])
def test_nand(a,b,expect):
    assert gate.Nand(a,b) == expect

テストの方はやや複雑に書いていますが、行なっているのは真理値表の入力に対して、expectsで定義した入力と一致しているか順番に確認していると言った感じになります。

これの結果が下記になります。

tests/test_gate.py::test_nand[0-0-1] PASSED
tests/test_gate.py::test_nand[0-1-1] PASSED
tests/test_gate.py::test_nand[1-0-1] PASSED 
tests/test_gate.py::test_nand[1-1-0] PASSED

無事にテストが通ったのでNANDの論理ゲートは正しく動いていることがわかりました。

NOTゲートを作る

NOTゲートは一つの入力に対し、反転した値を出力する論理ゲートです。

in	out
0	1
1	0

NOTゲートをNANDゲートだけで考えてみる

私の場合まず図で考えてみることにしました。

図で表現すると下記の通りでNOTは表現できます。

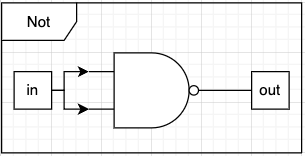
INの値をa,b両方に入れる感じですね。

これを真理値表で表現すると次のようになります。

in	a	b	NAND(a,b)
0	0	0	1
1	1	1	0

inの値が反対になっているのでNOTの動きになっていますね。

この図は合っていそうです。

プログラミングで実装してみる

次にpythonで上の図と照らし合わせながら、実装してみました。

テストも併せて実装しています。

def Not(a:bool) -> bool:
    out = Nand(a,a)
    return out

# ... 省略

in1 = list(itertools.product([0,1],repeat=1))
expects = [1,0]
@pytest.mark.parametrize("a,expect",
   [x + (y,) for x, y in zip(in1, expects)])
def test_not(a,expect):
    assert gate.Not(a) == expect

tests/test_gate.py::test_not[0-1] PASSED
tests/test_gate.py::test_not[1-0] PASSED

無事にNANDだけでNOTも作ることができました。

他の論理ゲートも同じような流れで作成していきます。

ANDゲートを作る

ANDゲートは２つの入力を受け取り、両方の入力1なら出力を1にする論理ゲートです。

真理値表は次のようになります。

a	b	out
0	0	0
0	1	0
1	0	0
1	1	1

真理値表を見るとNANDと0と1がひっくり返ったものになります。

そもそもNANDがNot ANDから来ているのでこの関係性は頷けるものかと思います。

NANDからANDにするにはもう一度ひっくり返せばOKです。つまり、出力にNOTゲートをくっ付ければ作ることができます。

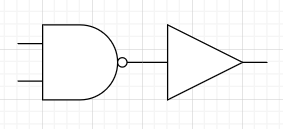
なお、前述の通りNOTゲートはNANDで作ることができましたので、NANDで作られたNOTゲートを使用して実装していきます。一度できたものは有効活用していきます。

ANDゲートの実装

def And(a:bool,b:bool) -> bool:
    in1 = Nand(a,b)
    out = Not(in1)
    return out

expects = [0,0,0,1]
@pytest.mark.parametrize("a,b,expect",
   [x + (y,) for x, y in zip(in2, expects)])
def test_and(a,b,expect):
    assert gate.And(a,b) == expect

tests/test_gate.py::test_and[0-0-0] PASSED
tests/test_gate.py::test_and[0-1-0] PASSED
tests/test_gate.py::test_and[1-0-0] PASSED
tests/test_gate.py::test_and[1-1-1] PASSED

ORゲートを作る

ORゲートは２つの入力を受け取り、片方の入力1なら出力を1にする論理ゲートです。

真理値表は次のようになります。

a	b	out
0	0	0
0	1	1
1	0	1
1	1	1

NANDで構成する場合は以下のようになります。

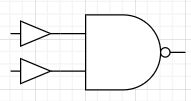
各入力前の値をNOTゲートで反転するとORになります。

NOTは前述の通り作成済みですのでそのまま利用しましょう。

ORゲートの実装

def Or(a:bool,b:bool) -> bool:
    in1 = Not(a)
    in2 = Not(b)
    out = Nand(in1, in2)
    return out

expects = [0,1,1,1]
@pytest.mark.parametrize("a,b,expect",
   [x + (y,) for x, y in zip(in2, expects)])
def test_or(a,b,expect):
    assert gate.Or(a,b) == expect

tests/test_gate.py::test_or[0-0-0] PASSED
tests/test_gate.py::test_or[0-1-1] PASSED
tests/test_gate.py::test_or[1-0-1] PASSED
tests/test_gate.py::test_or[1-1-1] PASSED

以上から無事にNANDの作成、及び基本の論理ゲートに当たる、NOT ,AND,ORをNANDから作成することができました。

作ってみた感想ですが、基本的な構成要素から組み合わせて別の新しいものを作り出す、そして作り出したものを使いながらより複雑なものが作れるようになる、と言った感触が自分には向いているらしく、空き時間を使いながら夢中で取り掛かれました。

この後も、XORだったりマルチプレクサだったりを作ってみようかなと考えています。最終的には参考書籍のようにNANDからテトリスまで作り上げてみたいですね。

それではこの辺で、またお会いしましょう。

*1:NORゲートもですが

cacapon’s diary

NAND論理ゲートから他の論理ゲートを作ってみる　その１